Etats mentaux

Sans entrer dans les détails pour l'instant, nous utiliserons dans la suite une logique modale. La base de connaissances d'un agent sera un ensemble d'expressions qui utilisent des modalités pour typer les états mentaux (croyances, désirs, ...). On pourra par exemple utiliser les modalités du tableau 2.1.

 

Tableau 2.1: Exemples de modalités

Modalité	Exemple	Signification
B	Bxp	L'agent x croit p
MB	MBx,yp	Les agents x et y croient mutuellement p
KIF	KIFxp	L'agent x sait si p
K	Kxp	L'agent x sait p
W	Wxp	L'agent x désire que p devienne vrai

 

Il existe plusieurs axiomatiques possibles utilisant cette logique modale. Il faut tout d'abord remarquer que ces modalités ne sont pas toutes indépendantes. On a en effet :

$$\left\{ \begin{array}{l} MB_{x,y}p \equiv B_xp \land B_yp \... ... \\ KIF_xp \equiv B_xp \lor B_x \lnot p \end{array} \right.$$

Il est important de remarquer que la croyance mutuelle ne peut pas être considérée comme un état mental. En effet, sa définition fait intervenir les deux agents simultanément. Donc si l'on veut éviter l'utilisation de structures partagées^2.2, il faudra considérer des croyances sur ce que sont les croyances mutuelles : B_xMB_x,yp.

Le savoir K est une modalité plus forte que la croyances B. On ne peut savoir que des choses qui sont vraies alors que les croyances peuvent être en conflit avec l'état du monde.

En ce qui concerne les axiomatiques, on évoquera rapidement le système S5 (voir [Chellas, 1980]) par exemple. Ce système, adapté à notre domaine d'application pour modéliser les croyances, peut s'écrire :

(K)	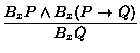$$\frac{B_xP \land B_x(P \to Q)}{B_xQ}$$
(T)	$$\frac{K_xP}{P}$$
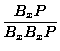(4)	$$\frac{B_xP}{B_xB_xP}$$	(introspection positive)
(5)	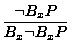$$\frac{\lnot B_xP}{B_x \lnot B_xP}$$	(introspection négative)

L'axiome (T) ne s'applique pas à la croyance, alors que les axiomes (K), (4) et (5) s'appliquent aussi au savoir.

Ce système de règles est bien adapté à la croyance, mais il existe d'autres modalités, dont l'intention (modalité W). Dans la suite, on présentera une approche intentionnelle de la modélisation d'agents. L'intention doit donc pouvoir être produite et utilisée par des règles.

(W+)	$$\frac{W_xKIF_xQ \land B_x(P \to Q)}{W_xKIF_xP}$$	(apparition directe d'une intention)
(W+')	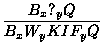$$\frac{B_x?_yQ}{B_xW_yKIF_yQ}$$	(apparition d'une croyance sur les intentions de l'autre agent) 2.1
(W-)	$$\frac{KIF_xQ}{\lnot W_xKIF_xQ}$$	(disparition d'une intention)

Ces règles expriment l'apparition et la disparition d'intentions particulières, à savoir l'intention de connaître la valeur de vérité d'une formule.